
The Science behind the GMEG
We live on an amazing planet. We have a rocky world to call our home on which we live.
Around us, the sun gives us warmth, we have air to breathe and a breeze to cool us down, we have water to drink, we have food and we have gravity to keep us neatly in place on earth. Perfect right?
Our craving for electricity just keeps growing with increased demand, and our reliance on fossil fuels is putting us on a trajectory that will only mean big trouble for our planet.
We have learned how to extract energy from our natural environment,. We now have solar panels, wind turbines, biofuel and hydro power gravity-based machines to name a few.

Gravity
Since Isaac Newton gave us a greater understanding of not only earth's gravity, but gravity all around us in this massive universe, we have learned quickly,
Earth's gravity attracts at a force of 9.8 meter per second squared. Isaac gave us a neat formula, W=mg. Here, “W” is the weight of an object measured in Newton, “m” is the mass of an object let's say 1 kilogram, and “g” is the acceleration due to gravity which is 9.8 meters per second squared .
As per his observantion, a 1 kilogram object will have a weight of 9.8 Newton in the air.
We understand gravity's influence when we move things around and how hard we have to work to do that. We can move things from one place to another, how to swing things around, make them go forward or backwards or upwards or downwards. And everything has its own energy cost. We have learned the parameters in which things work and therefore the law of physics.
The same as a hydro-electric generator, the Gravitational Mechanical Energy Generator delivers mechanical energy from the downward pull of the force of gravity.
Back to basics
Lifting objects
The law of gravity states that earth's gravity pulls on everything wih a downward force of approxamitely 9.8 meters per second. Therefore, if I lift 1 kilogram 1 meter from the ground into the air over 1 second, I will expend 9.8 Joules, or 9.8 Watts.
E = Fd = (ma)d = mgd = (1 kg)(9.8m/s2)(1 m) = 9.8 kg m2/s2 = 9.8 joules or 9.8 watts
Gravity Energy Storage
We are currently using gravity to store excess energy we can use at a later point.
We first lift a very heavy block high up into the air, thereby giving it gravitational potential energy. This happens everytime we pick something up. When we need it, we can lower the block, which will pull against a generator to produce electricity.
This energy system is equal. as the maximum power we can get out is the amount of energy it costed us to lift it up, less some inefficiencies.

The gravitational pull
Wherever there is a small decline in a surface, gravity will do its best to start pulling on any object.
That is why, when we go Zorbing or pull a ball at the top of a hill, it will automatically start rolling down. If not stopped in any way, the ball will continue to roll until it reaches the bottom, and will most likely come to a standstill.
It can roll down on its own, but it cannot roll up again on it own, due to gravity.

The GMEG
The GMEG (Gravitational Mechanical Energy Generator) relies on this simple and always dependable law of nature to be powered.
We call it a Gravity Enabler. This the device that hosts hanging weights.
When released on a downward track, the gravity enabler runs downwards powered by the force of gravity, providing a pulling force through the hanging weights, which will in turn pull a cable and can deliver mechanical energy.
Our second example of a gravity based machine!
Motion
Within the laws of physics, we can apply different motions to objects, each with their own energy requirement and different from each other

We can move objects up or down

We can move things left or right

A see saw acts as a 2 point mass system which can be tilted to the left or the right
Speeding things up through a gear system
We have created machines capable of lifting incredibly heavy objects around based on this principle. And that is how much of our current work is done.
Machines can only output a little less than you put in, and that energy must come from somewhere. And when you speed things up, you must put in even more energy in when using something like a gear system.

Increased rotational conversion
If 6 of us is needed to turn a wheel, which is connected to an output wheel that is 6 times smaller than our wheel, we will only have the power of 1 person to use on the smaller wheel to do work. This means to get a 1 kilogram force out 6 times per second, you will need to put in a 6 kg force once per second.

Magnetic Generators
Magnetic generators are renewable energy sources with no carbon footprint when generating electricity. It works by simply rotating magnets across copper wires.

Operational Torque
Magentic generators have what is called an operational torque. Part of what we have learned so far is that it takes a bit of effort to get something spinning, but the longer you spin it at the same speed, the less energy is needed to keep it going.
Speed has a huge part to play here. It does not matter how much power you want the magnetic generator to put out, whether it be 1 kW or 5 kW or 15 kW.
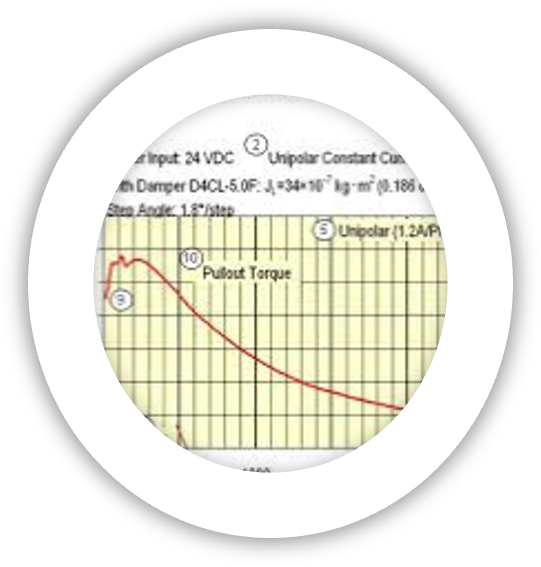
Operational Torque = Watt
When the operational torque is divided by the generator output power, at a certain speed you more or less need the same operational torque for continious operation..
Newton-meter input requirement per Watt
70 – 220 RPM = 0.0424 Nm
300 – 360 RPM = 0.03 Nm
500 – 600 RPM = 0.022 Nm

Hanging weights = operational torque
The Gravitational Mechanical Energy Generator relies on this operational torque for electricity generation.
By connecting an increased rotational conversion system, and by applying the power requirement based on ration ratio, any denomination of hanging weights can be added to deliver any given Watt.


.jpg)